isosceles

triángulo isósceles

Triángulo en el que al menos dos lados son congruentes. A los lados congruentes se les llama catetos. El ángulo formado por los catetos es el ángulo vértice. Los otros dos ángulos son los ángulos base. La base es el lado opuesto al ángulo vértice.

---

semejanza de triangulos y teoreme de tales

semejanza de triangulos

Los lados a y a', b y b', c y c' se llaman lados homólogos.

Son ángulos homólogos:

Dos triángulos son semejantes cuando tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales.

La razón de la proporción entre los lados de los triángulos se llama razón de semejanza.

La razón de los perímetros de los triángulos semejantes es igual a su razón de semejanza.

La razón de las áreas de los triángulos semejantes es igual al cuadrado de su razón de semejanza.

teorema de tales

Primer teorema

Una aplicación del Teorema de Thales.

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:

Teorema primero Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes. Tales de Mileto

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.

Segundo teorema

fig 2.1 Ilustración del enunciado del segundo teorema de Tales de Mileto.

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Teorema segundo Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el ángulo ABC, es recto. Tales de Mileto

Este teorema (véase fig 2.1 y 2.2), es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.

tres demostraciones de los tres criterios de congruencia

En geometría, dos conjuntos de puntos son congruentes (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es combinación de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.



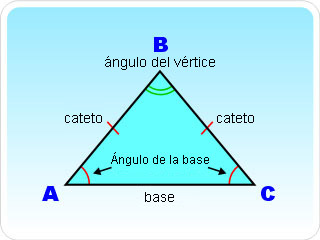
 Congruencia de triángulosDos triángulos son congruentes si sus ángulos correspondientes tienen la misma medida, y sus lados homólogos miden lo mismo. Sin embargo, para construir un triángulo congruente, es necesario conocer tres de sus medidas, y uno de esos datos debe ser la medida de un lado.
Como los elementos primarios de los triángulos (ángulos y lados) son dependientes, la información mínima necesaria para que los triángulos sean congruentes responde a los llamados criterios de congruencia:

Criterios de congruencia de triángulos
1. Criterio (L, L, L)
Dos triángulos son congruentes si sus lados correspondientes son congruentes:

2. Criterio (L, A, L)Dos triángulos son congruentes si tienen dos lados correspondientes y el ángulo comprendido entre ellos congruentes.

3. Criterio (A, L, A)Dos triángulos son congruentes si tienen dos ángulos correspondientes y el lado comprendido entre ellos congruentes.

porque los angulos interiores de un triangulo suman 180 grados

Porque un triángulo es un polígono, en el cual hace los tres lados determinados por esos tres segmentos de las tres rectas se corten, por el cual si al triángulo se lo pone todos sus lados en líneas rectas formaría un ángulo llano (el cual es de 180°), por este motivo tendrán que dar la suma de sus ángulos 180°.
Toma en cuenta estás consideraciones que debe cumplir el triángulo:

*En todo triángulo, la suma de los ángulos interiores es igual a dos rectos.
*En todo triángulo, un ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes.
*Dos triángulos son iguales cuando tienen iguales un lado y sus dos ángulos adyacentes.
*Dos triángulos son iguales cuando tienen dos lados iguales y el ángulo comprendidos.
*Dos triángulos son iguales cuando tienen los tres lados iguales.
*En todo triángulo, a mayor lado se opone mayor ángulo.
*Si un triángulo tiene dos lados iguales, sus ángulos opuestos son también iguales.
*En todo triángulo, un lado es menor que la suma de los otros dos y mayor que su diferencia.

angulos adyacentes y congruencia de triangulos

Ángulos adyacentes.

Ángulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.

La congruencia de triángulos estudia los casos en que dos o más triángulos presentan ángulos de igual medida o congruentes, así como lados de igual medida o congruentes.

 Condiciones de congruencia

Para que se dé la congruencia de dos o más triángulos, se requiere que sus lados respectivos sean congruentes, es decir que tengan la misma medida. Esta condición implica que los ángulos respectivos también tienen la misma medida o son congruentes. Las figuras congruentes son aquellas que tienen la misma forma y el mismo tamaño. Las partes coincidentes de las figuras congruentes se llaman homologas o correspondientes.

 Criterios de congruencia de triángulos

Dos triángulos son congruentes cuando sus tres lados y ángulos también lo son, sin embargo, puede demostrarse la congruencia de dos triángulos si se sabe que algunas de sus partes correspondientes son homólogas

caracteristicas de 2 triangulos

 triángulo equilátero, es un triángulo con tres lados iguales. En la geometría euclídea tradicional, los triángulos equiláteros también son equiangulares, es decir, los tres ángulos internos también son congruentes entre sí, cada ángulo vale 60°. Un triángulo equilátero es un polígono regular; es un caso especial de triángulo isósceles.

Triángulo Escaleno
	Un triángulo con todos los lados de diferentes longitudes. Ningún lado es igual a otro ni ningún ángulo es igual a otro.

angulos alternos internos, externos

Ángulos alternos internos

Si una recta transversal corta a dos rectas paralelas, los ángulos alternos internos son los que están entre las paralelas a distinto lado de ellas y a distinto lado de la transversal.

Los ángulos 2 y 3 son iguales.

Ángulos alternos externos

Si una recta transversal corta a dos rectas paralelas, los ángulos alternos externos son los que están en la parte exterior de las paralelas a distinto lado de ellas y a distinto lado de la transversal.

Los ángulos 1 y 4 son iguales.

angulos correspondientes y opuestos por el vertice

Ángulos correspondientes

Cuando dos líneas se cruzan con otra (que se llama transversal), los ángulos en las esquinas correspondientes se llaman ángulos correspondientes. En este ejemplo, son ángulos correspondientes: a y e b y f c y g d y h

Ángulos opuestos por el vértice

Ángulos opuestos por el vértice son aquellos cuyos lados de uno son semirrectas opuestas a los lados del otro.
Los vértices de ambos ángulos son comunes y sus lados están en un par de rectas que se cortan en el vértice común, pero no poseen ningún punto interior común.

4cm, 5cm, 9 cm se poda crearv un triangulo?
no, porque las longitudes de los lados deben de ser mayor que la tercera
una linea de 5 y una de 6 cm la mitad es de 2.5

tipos de angulos que se forman en dos rectas paralelas cortadas con una secante...caracteristicas de cada uno de los angulos anteriores

Al cortar dos rectas con una secante se forman ocho angulos, los cuales se representan por letras minusculas; estos se clasifican por parejas de acuerdo con la posicion que tienen con la secante.

1. angulos colaterales internos: son los angulos que se encuentran del mismo lado de la secante y dentro de las rectas.
Los angulos colaterales internos son:

angulos colaterales externos: son aquellos que se encuentran del mismo lado de la secante y fuera de las rectas.
Los angulos colaterales externos, son:

angulos correspondientes: son los angulos que se encuentran en un mismo lado de la secante, formando parejas, un interno con un externo.
Los angulos correspondientes son:

angulos alternos internos: son los angulos interiores que se encuentran en uno y otro lado de la secante.
Los angulos alternos internos:

angulos alternos externos: son los angulos exteriores que se encuentran en uno y otro lado de la secante.
Los angulos alternos externos son:

angulos opuestos por el vertice: son aquellos que tienen en comun el mismo vertice y se oponen uno al otro.
Los angulos opuestos por el vertice son:

2.

3.

4.

5.

6.

Si las rectas cortadas por la secante son paralelas, los angulos tienen las siguientes relaciones:

1. Los angulos colaterales son suplementarios, esto es, suman 180�:

Los angulos correspondientes tienen la misma medida, es decir , son congruentes:

Los angulos alternos tienen igual medida, es decir , son congruentes:

Los angulos opuestos por el vertice tienen igual medida, esto es son congruentes:

Si se traza una secante a dos rectas paralelas y se conoce la medida de uno de los angulos, es posible determinar la medida de los otros.
Observese el siguiente ejemplo:

Como los angulos colaterales son suplementarios y los angulos e y h son colaterales, entonces:

Los angulos correspondientes son congruentes, por lo tanto:

entonces,

Los angulos alternos son congruentes entonces:

por lo tanto:

2.

3.

4.